Autres propriétés de la suite de Fibonacci

 

Nombres premiers de la suite de Fibonacci :

n	Fn	=	Facteurs
0	0
1	1
2	1
3	2	P	(P=Premier)
4	3	P
5	5	P
6	8		2³
7	13	P
8	21		3x7
9	34		3²
10	55		5x11
11	89	P
12	144		24x3²
13	233	P
14	377		13 x 29
15	610		2 x 5 x 61
16	987		3 x 7 x 47
17	1 597	P
18	2 584		2³ x 17 x 19
19	4 181		37 x 113
20	6 765		3 x 5 x 11 x 41
...	Les "premiers" suivants
23	28 657	P
29	514 229	P
43	433 494 437	P
47	2 971 215 073	P
83	99 194 853 094 755 497	P
	100ème terme
100	354 224 848 179 261 915 075		*
* 354 224 848 179 261 915 075 = 3 . 5² . 11 . 41 . 101 . 151 . 401 . 3001 . 570 601 = 3,5 1020

N.B: à partir de 5, F_n n'est premier que si n est premier

 

Fn + Fn+1 + ... + Fn+10 = 11 x Fn+7

Fn+2 = F1 + F2 + ... + Fn + 1

F2n+1 = F1 + F2 + F4 + F6 ... + F2n

Fn et Fn+1 sont premiers entre eux

Fn² = F_n-1 x F_n+1 + (-1)^n-1

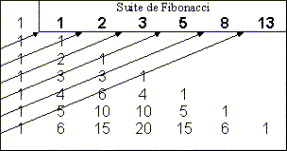
Dans le triangle de Pascal, la somme des "diagonales" sont des suites de Fibonacci :

F_n ² + F_n+1 ² = F_2n+1